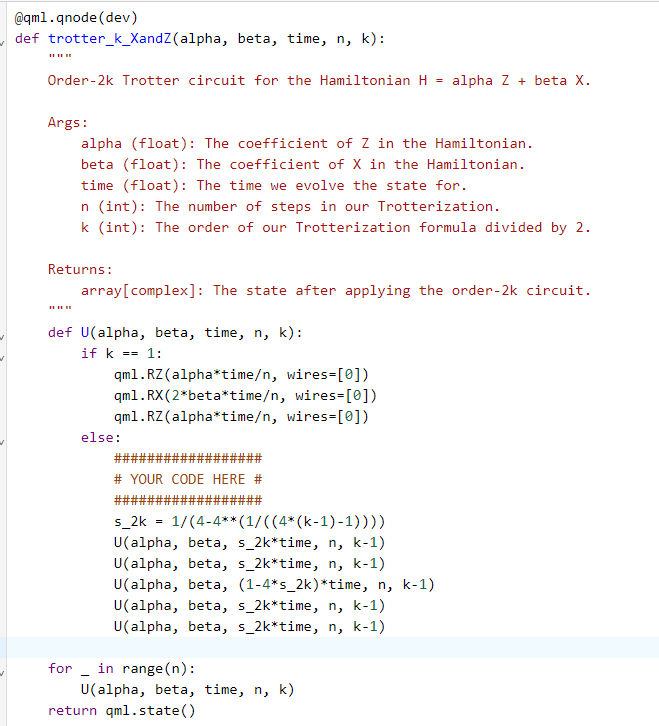
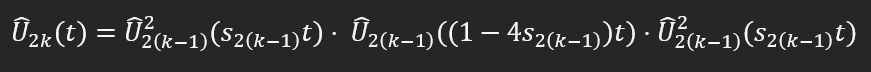Hi. Im so stuck on this chapter.
Also, it seems there may be an error in the theory section under Higher-order Trotterization.
Hi! thanks for this question.
I’m so glad you are working through the Codebook.
I think you found a mistake, but the solution is rather s_{2k}=1/(1-4^{1/(2k+1)}). I found the correct formula in a reference.
I will fix this both in the theory and the Codercises. Your codercise solution will be almost correct, you just need to change s_2k to the correct value that we just discussed.
Check back in a few days and things should be working properly.
Thank you again for spotting these mistakes and reporting them.
I see. Thanks! I was losing my head over this.
No worries, i really enjoy doing the exercises. Even though sometimes im losing my mind over the math, im really having a blast learning something this exciting
I think i see the issue the formula for s_2k is 1/(4-4^(1/(2k+1))), but the k is for the 2k order, as in when k = 2, the order is 4, therefore the s used is 1/(4-4^(1/(2(k-1)+1))) which equals to 1/(4-4^(1/(2k-1))).
This
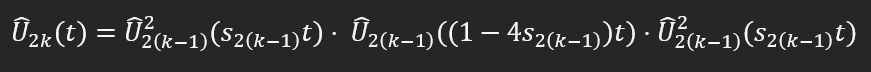
would be more accurate if we are to use the correct formula in the reference as you mentioned.
For U_2k, s_2(k-1) = 1/(4-4^(1/(2(k-1)+1))) = 1/(4-4^(1/(2k-1))), which when k=2, s_2 = 1/(4-4^(1/(3)))
I also found this module, let alone codercise challenging. Like @cyyoung, I had implemented
s_2k = 1 / (4 - 4**(1 / (2*k - 1)))
but I’m still incorrect.. I’ve implemented the same lines of recursion as well.
Hi!
Thanks for the feedback. Is there anything in particular that you think we can improve to make it more understandable?
Regarding your question, the formula both in the theory and the codercise is s_2k = 1 / (4 - 4**(1 / (2*k + 1))). There is a plus one and not minus one. This one should work, let me know.
Oh I see now.. I got confused between the discussions of s_2k but needed to pay attention to whether it was + or - for the correct formula. The small details are killer!
Thank you Daniela!
Hi! I just finished the code excercise and I think the issue hasn’t been fixed yet! I think the source of confusion is that there are two equivalent ways the Suzuki recursion is sometimes written, depending on whether you define U_{2k} from U_{2(k-1)} or U_{2(k+1)} from U_{2k}.
If the order-2k formula is defined recursively from the order-2(k-1) formula:
with
This form can be found in qml.TrotterProduct — PennyLane 0.42.3 documentation
But if you instead write the recursion as building U_{2(k+2)} directly from U_{2k}, then the coefficient takes the form
Both formulas are correct, but they are shifted by the index convention: one defines U_{2k} from U_{2(k-1)}, while the other defines U_{2(k+2)} from U_{2k}.
In the exercise code, the recursion function U(..., k) is meant to build U_{2k} out of U_{2(k-1)}. In that case, the correct coefficient should be
not with 2k+1. Using 2k+1 corresponds to the other indexing convention (jumping by 2 each time), which doesn’t match how the code is structured. On the other hand, the formula of the theory part in the Codebook is still correct since the plus one form is for building U_{2(k+2)} from U_{2k}.
Thanks for your input, @petrus1732 !!
Let me take a careful look and get back to you.
Just out of curiosity, was there a typo in your answer and you meant U_{2(k+1)} instead of U_{2(k+2)}? (in the second half).
Yes, that’s a typo. Sorry for the confusion.
Hi!
I think I finally see what you are saying.
The conventions got mixed up. The theory part is consistent and correct in itself. But the Codercise is built with the recursion of the k-1 unitaries and the correct thing to do would be to keep 2k-1 in the s variable there. Ah! this is unfortunate.
I will also change the statement of the codercise to be consistent with the implementation.
Thanks. I will get to it asap.
Hi! please see the latest discussion on this topic so things can be further clarified. Sorry about the confusion and thanks for participating in the forum.
