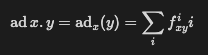Hi
I was using the demos on Lie algebra to introduce myself to the topic and they have been of great help. However, in the tutorial on g-sim the adjoint identity is mentioned as
However, in a talk given by Dr. Kottmann on the topic (https://www.youtube.com/watch?v=rMyC83m1r3M) the following form was mentioned as well.
To me these seem different (where the first represents the exponential of the matrix elements and the second the matrix elements of the exponential), where the second one makes more sense to me. Could somebody explain how these equations are equivalent?
Thanks in advance
Kind regards
Ruben
Hi @ruvdrsti , welcome to the Forum!
They seem the same to me. If you look at the line just below the definition of the adjoint identity in the g-sim demo, you will see that the adjoint representation of the associated Lie algebra is given by the structure constants f as shown in the equation below:
If you see Lemma 3.14 in Introduction to Lie Groups and Lie Algebras you’ll see that ad\ x.y = [x,y] .
If you look at the g-sim demo you’ll see that the commutator can be decomposed as a linear combination of other elements in g, where the coefficients are the structure constants f.
So it looks to me that both equations in your question are actually the same.
Hi @CatalinaAlbornoz Thank you for your reply.
I am still a bit confused. I had interpreted the adjoint as being a matrix, and then Lemma 3.14 becomes
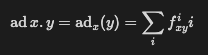
However, the index i goes over all elements of the Lie algebra. From here, I don’t see the link between ad_x(y) and the matrix elements of the adjoint [ad_x]_{ij}. That is why I assumed that

Could you help me in understanding this link between ad_x(y) and [ad_x]_{ij}?
EDIT: apologies for the Latex code, I have not figured out how this works in this forum.
Hi @ruvdrsti ,
Note that ad is a map of lie algebras as defined in Lemma 3.14. Pages 24 and 25 contain a lot of the definitions and examples that may help to clarify things.
I’m not sure how you derived the first equation above. What theorems or equations does this come from? Maybe this can help clarify the confusion too.
No worries about the LaTex code. All you need is adding a $ sign at the beginning and end of your mathematical expression. E.g. ad_x(y) then renders as ad_x(y).
I hope this helps!
Hi @CatalinaAlbornoz
Since I’m not sure which part of the equation you are talking about;
The first equation (the first half) is the definition of the adjoint of a Lie algebra element on the wikipedia page linked in the demo (under the heading ‘Adjoint representation of a Lie algebra’). Given the similarity of the definition given there and in Lemma 3.14 I assumed they were the same.
The second part is the linear combination you mentioned in your last comment.
I think I understand the meaning of the adjoint better, but I still don’t get why it does not matter that the indices \\alpha and \\beta appear inside or outside the exponential.
Hi @ruvdrsti ,
I think I understand the confusion now.
When Korbinian wrote e^{-i\theta (ad_{h_u})_{\alpha \beta}} that just meant e_{\alpha \beta}^{-i\theta ad_{h_u}}.
And since (ad_{h_u})_{\alpha \beta}=f_{\alpha \beta}^{\mu} then you see why e_{\alpha \beta}^{-i\theta ad_{h_u}}=e^{-i\theta f_{\alpha \beta}^{\mu}}.
Let me know if this clarifies things.
Hi @CatalinaAlbornoz
Yes, I get it now. Thanks a lot for your help!
1 Like
Hi @ruvdrsti
Your question is totally valid and also had me confused for a while. The answer is short:
It is the elements of the matrix exponential, not the exponential of the matrix elements.
(e^{-i \theta \ ad_{h_\mu} })_{\alpha \beta} = (e^{-i \theta f^{\mu}})_{\alpha \beta}
The notation in the demo is indeed misleading, will need to change that!
2 Likes
Hi @Qottmann
Thank you for clarifying!
1 Like