Adam Optimizer Cost Function doesn't change values in training

PennyLane Help Code Together
1

I am using this tutorial on QNN code to predict inflation through the CPI values using this dataset on Kaggle. X- Axis is the Year and Y-axis is CPI. I have normalized the CPI values -
CPI[:] = CPI[:]/np.linalg.norm(CPI[:])
image
The issue is the Adam optimizer cost function isn’t changing it’s values, as shown in the snippet below. What am I missing?

opt = AdamOptimizer(0.001, beta1=0.9, beta2=0.999)

var = var_init

for it in range(5):
    var, _cost = opt.step_and_cost(lambda v: cost(v, X, Y), var)
    print("Iter: {:5d} | Cost: {:0.7f} ".format(it, _cost))

Iter: 0 | Cost: 0.0012674
Iter: 1 | Cost: 0.0012674
Iter: 2 | Cost: 0.0012674
Iter: 3 | Cost: 0.0012674
Iter: 4 | Cost: 0.0012674

2

Hey @NolanCMas, welcome to the forum!

I wasn’t able to replicate your error. Copy-pasting the code from the URL you linked, here is my output. Note that I deleted import numpy as np since you already imported it via PennyLane and I used a dummy dataset since I don’t have sine.txt.

import pennylane as qml
from pennylane import numpy as np
from pennylane.optimize import AdamOptimizer
import matplotlib.pyplot as plt

import pylab
import matplotlib as mpl

X = np.random.uniform(0, 1, size=10, requires_grad=False)
Y = np.random.uniform(0, 1, size=10, requires_grad=False)

dev = qml.device("strawberryfields.fock", wires=1, cutoff_dim=10)

def layer(v):
    # Matrix multiplication of inputs
    qml.Rotation(v[0], wires=0)
    qml.Squeezing(v[1], 0.0, wires=0)
    qml.Rotation(v[2], wires=0)

    # Bias
    qml.Displacement(v[3], 0.0, wires=0)

    # nonlinear transformation
    qml.Kerr(v[4], wires=0)

@qml.qnode(dev)
def quantum_neural_net(var, x=None):
    # Encode input x into a quantum state
    qml.Displacement(x, 0.0, wires=0)

    #call layer(v) which will be the subcircuit of the variational circuit of the neural network
    for v in var:
        layer(v)

    return qml.expval(qml.X(0))

def square_loss(labels, predictions):
    loss = 0
    for l, p in zip(labels, predictions):
        loss = loss + (l - p) ** 2

    loss = loss / len(labels)
    return loss

def cost(var, features, labels):
    preds = [quantum_neural_net(var, x=x) for x in features]
    return square_loss(labels, preds)

np.random.seed(0)
num_layers = 4
var_init = 0.05 * np.random.randn(num_layers, 5)

opt = AdamOptimizer(0.01, beta1=0.9, beta2=0.999)

var = var_init
for it in range(3):
    var, _cost = opt.step_and_cost(lambda v: cost(v, X, Y), var)
    print("Iter: {:5d} | Cost: {:0.7f} ".format(it, _cost))

'''
Iter:     0 | Cost: 0.3720478 
Iter:     1 | Cost: 0.2624777 
Iter:     2 | Cost: 0.1864948 
'''

It could be that you need to update PennyLane. You can do so via pip install --upgrade pennylane. Does that solve the issue?

3

Thank you for the quick response. I upgraded the pennylane library, but there’s no change.
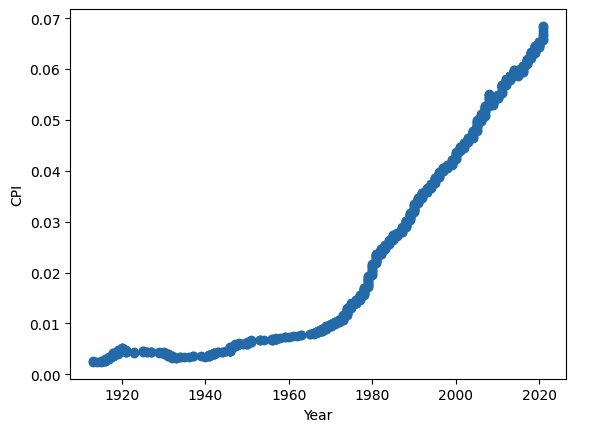
Here’s the dataset: X, Y axis. <sorry unable to attach this as a csv/txt)
Year,CPI
1913,9.8
1913,9.8
1913,9.8
1913,9.8
1913,9.7
1913,9.8
1913,9.9
1913,9.9
1913,10
1913,10
1913,10.1
1913,10
1914,10
1914,9.9
1914,9.9
1914,9.8
1914,9.9
1914,9.9
1914,10
1914,10.2
1914,10.2
1914,10.1
1914,10.2
1914,10.1
1915,10.1
1915,10
1915,9.9
1915,10
1915,10.1
1915,10.1
1915,10.1
1915,10.1
1915,10.1
1915,10.2
1915,10.3
1915,10.3
1916,10.4
1916,10.4
1916,10.5
1916,10.6
1916,10.7
1916,10.8
1916,10.8
1916,10.9
1916,11.1
1916,11.3
1916,11.5
1916,11.6
1917,11.7
1917,12
1917,12
1917,12.6
1917,12.8
1917,13
1917,12.8
1917,13
1917,13.3
1917,13.5
1917,13.5
1917,13.7
1918,14
1918,14.1
1918,14
1918,14.2
1918,14.5
1918,14.7
1918,15.1
1918,15.4
1918,15.7
1918,16
1918,16.3
1918,16.5
1919,16.5
1919,16.2
1919,16.4
1919,16.7
1919,16.9
1919,16.9
1919,17.4
1919,17.7
1919,17.8
1919,18.1
1919,18.5
1919,18.9
1920,19.3
1920,19.5
1920,19.7
1920,20.3
1920,20.6
1920,20.9
1920,20.8
1920,20.3
1920,20
1920,19.9
1920,19.8
1920,19.4
1921,19
1921,18.4
1921,18.3
1921,18.1
1921,17.7
1921,17.6
1921,17.7
1921,17.7
1921,17.5
1921,17.5
1921,17.4
1921,17.3
1922,16.9
1922,16.9
1922,16.7
1922,16.7
1922,16.7
1922,16.7
1922,16.8
1922,16.6
1922,16.6
1922,16.7
1922,16.8
1922,16.9
1923,16.8
1923,16.8
1923,16.8
1923,16.9
1923,16.9
1923,17
1923,17.2
1923,17.1
1923,17.2
1923,17.3
1923,17.3
1923,17.3
1924,17.3
1924,17.2
1924,17.1
1924,17
1924,17
1924,17
1924,17.1
1924,17
1924,17.1
1924,17.2
1924,17.2
1924,17.3
1925,17.3
1925,17.2
1925,17.3
1925,17.2
1925,17.3
1925,17.5
1925,17.7
1925,17.7
1925,17.7
1925,17.7
1925,18
1925,17.9
1926,17.9
1926,17.9
1926,17.8
1926,17.9
1926,17.8
1926,17.7
1926,17.5
1926,17.4
1926,17.5
1926,17.6
1926,17.7
1926,17.7
1927,17.5
1927,17.4
1927,17.3
1927,17.3
1927,17.4
1927,17.6
1927,17.3
1927,17.2
1927,17.3
1927,17.4
1927,17.3
1927,17.3
1928,17.3
1928,17.1
1928,17.1
1928,17.1
1928,17.2
1928,17.1
1928,17.1
1928,17.1
1928,17.3
1928,17.2
1928,17.2
1928,17.1
1929,17.1
1929,17.1
1929,17
1929,16.9
1929,17
1929,17.1
1929,17.3
1929,17.3
1929,17.3
1929,17.3
1929,17.3
1929,17.2
1930,17.1
1930,17
1930,16.9
1930,17
1930,16.9
1930,16.8
1930,16.6
1930,16.5
1930,16.6
1930,16.5
1930,16.4
1930,16.1
1931,15.9
1931,15.7
1931,15.6
1931,15.5
1931,15.3
1931,15.1
1931,15.1
1931,15.1
1931,15
1931,14.9
1931,14.7
1931,14.6
1932,14.3
1932,14.1
1932,14
1932,13.9
1932,13.7
1932,13.6
1932,13.6
1932,13.5
1932,13.4
1932,13.3
1932,13.2
1932,13.1
1933,12.9
1933,12.7
1933,12.6
1933,12.6
1933,12.6
1933,12.7
1933,13.1
1933,13.2
1933,13.2
1933,13.2
1933,13.2
1933,13.2
1934,13.2
1934,13.3
1934,13.3
1934,13.3
1934,13.3
1934,13.4
1934,13.4
1934,13.4
1934,13.6
1934,13.5
1934,13.5
1934,13.4
1935,13.6
1935,13.7
1935,13.7
1935,13.8
1935,13.8
1935,13.7
1935,13.7
1935,13.7
1935,13.7
1935,13.7
1935,13.8
1935,13.8
1936,13.8
1936,13.8
1936,13.7
1936,13.7
1936,13.7
1936,13.8
1936,13.9
1936,14
1936,14
1936,14
1936,14
1936,14
1937,14.1
1937,14.1
1937,14.2
1937,14.3
1937,14.4
1937,14.4
1937,14.5
1937,14.5
1937,14.6
1937,14.6
1937,14.5
1937,14.4
1938,14.2
1938,14.1
1938,14.1
1938,14.2
1938,14.1
1938,14.1
1938,14.1
1938,14.1
1938,14.1
1938,14
1938,14
1938,14
1939,14
1939,13.9
1939,13.9
1939,13.8
1939,13.8
1939,13.8
1939,13.8
1939,13.8
1939,14.1
1939,14
1939,14
1939,14
1940,13.9
1940,14
1940,14
1940,14
1940,14
1940,14.1
1940,14
1940,14
1940,14
1940,14
1940,14
1940,14.1
1941,14.1
1941,14.1
1941,14.2
1941,14.3
1941,14.4
1941,14.7
1941,14.7
1941,14.9
1941,15.1
1941,15.3
1941,15.4
1941,15.5
1942,15.7
1942,15.8
1942,16
1942,16.1
1942,16.3
1942,16.3
1942,16.4
1942,16.5
1942,16.5
1942,16.7
1942,16.8
1942,16.9
1943,16.9
1943,16.9
1943,17.2
1943,17.4
1943,17.5
1943,17.5
1943,17.4
1943,17.3
1943,17.4
1943,17.4
1943,17.4
1943,17.4
1944,17.4
1944,17.4
1944,17.4
1944,17.5
1944,17.5
1944,17.6
1944,17.7
1944,17.7
1944,17.7
1944,17.7
1944,17.7
1944,17.8
1945,17.8
1945,17.8
1945,17.8
1945,17.8
1945,17.9
1945,18.1
1945,18.1
1945,18.1
1945,18.1
1945,18.1
1945,18.1
1945,18.2
1946,18.2
1946,18.1
1946,18.3
1946,18.4
1946,18.5
1946,18.7
1946,19.8
1946,20.2
1946,20.4
1946,20.8
1946,21.3
1946,21.5
1947,21.5
1947,21.5
1947,21.9
1947,21.9
1947,21.9
1947,22
1947,22.2
1947,22.5
1947,23
1947,23
1947,23.1
1947,23.4
1948,23.7
1948,23.5
1948,23.4
1948,23.8
1948,23.9
1948,24.1
1948,24.4
1948,24.5
1948,24.5
1948,24.4
1948,24.2
1948,24.1
1949,24
1949,23.8
1949,23.8
1949,23.9
1949,23.8
1949,23.9
1949,23.7
1949,23.8
1949,23.9
1949,23.7
1949,23.8
1949,23.6
1950,23.5
1950,23.5
1950,23.6
1950,23.6
1950,23.7
1950,23.8
1950,24.1
1950,24.3
1950,24.4
1950,24.6
1950,24.7
1950,25
1951,25.4
1951,25.7
1951,25.8
1951,25.8
1951,25.9
1951,25.9
1951,25.9
1951,25.9
1951,26.1
1951,26.2
1951,26.4
1951,26.5
1952,26.5
1952,26.3
1952,26.3
1952,26.4
1952,26.4
1952,26.5
1952,26.7
1952,26.7
1952,26.7
1952,26.7
1952,26.7
1952,26.7
1953,26.6
1953,26.5
1953,26.6
1953,26.6
1953,26.7
1953,26.8
1953,26.8
1953,26.9
1953,26.9
1953,27
1953,26.9
1953,26.9
1954,26.9
1954,26.9
1954,26.9
1954,26.8
1954,26.9
1954,26.9
1954,26.9
1954,26.9
1954,26.8
1954,26.8
1954,26.8
1954,26.7
1955,26.7
1955,26.7
1955,26.7
1955,26.7
1955,26.7
1955,26.7
1955,26.8
1955,26.8
1955,26.9
1955,26.9
1955,26.9
1955,26.8
1956,26.8
1956,26.8
1956,26.8
1956,26.9
1956,27
1956,27.2
1956,27.4
1956,27.3
1956,27.4
1956,27.5
1956,27.5
1956,27.6
1957,27.6
1957,27.7
1957,27.8
1957,27.9
1957,28
1957,28.1
1957,28.3
1957,28.3
1957,28.3
1957,28.3
1957,28.4
1957,28.4
1958,28.6
1958,28.6
1958,28.8
1958,28.9
1958,28.9
1958,28.9
1958,29
1958,28.9
1958,28.9
1958,28.9
1958,29
1958,28.9
1959,29
1959,28.9
1959,28.9
1959,29
1959,29
1959,29.1
1959,29.2
1959,29.2
1959,29.3
1959,29.4
1959,29.4
1959,29.4
1960,29.3
1960,29.4
1960,29.4
1960,29.5
1960,29.5
1960,29.6
1960,29.6
1960,29.6
1960,29.6
1960,29.8
1960,29.8
1960,29.8
1961,29.8
1961,29.8
1961,29.8
1961,29.8
1961,29.8
1961,29.8
1961,30
1961,29.9
1961,30
1961,30
1961,30
1961,30
1962,30
1962,30.1
1962,30.1
1962,30.2
1962,30.2
1962,30.2
1962,30.3
1962,30.3
1962,30.4
1962,30.4
1962,30.4
1962,30.4
1963,30.4
1963,30.4
1963,30.5
1963,30.5
1963,30.5
1963,30.6
1963,30.7
1963,30.7
1963,30.7
1963,30.8
1963,30.8
1963,30.9
1964,30.9
1964,30.9
1964,30.9
1964,30.9
1964,30.9
1964,31
1964,31.1
1964,31
1964,31.1
1964,31.1
1964,31.2
1964,31.2
1965,31.2
1965,31.2
1965,31.3
1965,31.4
1965,31.4
1965,31.6
1965,31.6
1965,31.6
1965,31.6
1965,31.7
1965,31.7
1965,31.8
1966,31.8
1966,32
1966,32.1
1966,32.3
1966,32.3
1966,32.4
1966,32.5
1966,32.7
1966,32.7
1966,32.9
1966,32.9
1966,32.9
1967,32.9
1967,32.9
1967,33
1967,33.1
1967,33.2
1967,33.3
1967,33.4
1967,33.5
1967,33.6
1967,33.7
1967,33.8
1967,33.9
1968,34.1
1968,34.2
1968,34.3
1968,34.4
1968,34.5
1968,34.7
1968,34.9
1968,35
1968,35.1
1968,35.3
1968,35.4
1968,35.5
1969,35.6
1969,35.8
1969,36.1
1969,36.3
1969,36.4
1969,36.6
1969,36.8
1969,37
1969,37.1
1969,37.3
1969,37.5
1969,37.7
1970,37.8
1970,38
1970,38.2
1970,38.5
1970,38.6
1970,38.8
1970,39
1970,39
1970,39.2
1970,39.4
1970,39.6
1970,39.8
1971,39.8
1971,39.9
1971,40
1971,40.1
1971,40.3
1971,40.6
1971,40.7
1971,40.8
1971,40.8
1971,40.9
1971,40.9
1971,41.1
1972,41.1
1972,41.3
1972,41.4
1972,41.5
1972,41.6
1972,41.7
1972,41.9
1972,42
1972,42.1
1972,42.3
1972,42.4
1972,42.5
1973,42.6
1973,42.9
1973,43.3
1973,43.6
1973,43.9
1973,44.2
1973,44.3
1973,45.1
1973,45.2
1973,45.6
1973,45.9
1973,46.2
1974,46.6
1974,47.2
1974,47.8
1974,48
1974,48.6
1974,49
1974,49.4
1974,50
1974,50.6
1974,51.1
1974,51.5
1974,51.9
1975,52.1
1975,52.5
1975,52.7
1975,52.9
1975,53.2
1975,53.6
1975,54.2
1975,54.3
1975,54.6
1975,54.9
1975,55.3
1975,55.5
1976,55.6
1976,55.8
1976,55.9
1976,56.1
1976,56.5
1976,56.8
1976,57.1
1976,57.4
1976,57.6
1976,57.9
1976,58
1976,58.2
1977,58.5
1977,59.1
1977,59.5
1977,60
1977,60.3
1977,60.7
1977,61
1977,61.2
1977,61.4
1977,61.6
1977,61.9
1977,62.1
1978,62.5
1978,62.9
1978,63.4
1978,63.9
1978,64.5
1978,65.2
1978,65.7
1978,66
1978,66.5
1978,67.1
1978,67.4
1978,67.7
1979,68.3
1979,69.1
1979,69.8
1979,70.6
1979,71.5
1979,72.3
1979,73.1
1979,73.8
1979,74.6
1979,75.2
1979,75.9
1979,76.7
1980,77.8
1980,78.9
1980,80.1
1980,81
1980,81.8
1980,82.7
1980,82.7
1980,83.3
1980,84
1980,84.8
1980,85.5
1980,86.3
1981,87
1981,87.9
1981,88.5
1981,89.1
1981,89.8
1981,90.6
1981,91.6
1981,92.3
1981,93.2
1981,93.4
1981,93.7
1981,94
1982,94.3
1982,94.6
1982,94.5
1982,94.9
1982,95.8
1982,97
1982,97.5
1982,97.7
1982,97.9
1982,98.2
1982,98
1982,97.6
1983,97.8
1983,97.9
1983,97.9
1983,98.6
1983,99.2
1983,99.5
1983,99.9
1983,100.2
1983,100.7
1983,101
1983,101.2
1983,101.3
1984,101.9
1984,102.4
1984,102.6
1984,103.1
1984,103.4
1984,103.7
1984,104.1
1984,104.5
1984,105
1984,105.3
1984,105.3
1984,105.3
1985,105.5
1985,106
1985,106.4
1985,106.9
1985,107.3
1985,107.6
1985,107.8
1985,108
1985,108.3
1985,108.7
1985,109
1985,109.3
1986,109.6
1986,109.3
1986,108.8
1986,108.6
1986,108.9
1986,109.5
1986,109.5
1986,109.7
1986,110.2
1986,110.3
1986,110.4
1986,110.5
1987,111.2
1987,111.6
1987,112.1
1987,112.7
1987,113.1
1987,113.5
1987,113.8
1987,114.4
1987,115
1987,115.3
1987,115.4
1987,115.4
1988,115.7
1988,116
1988,116.5
1988,117.1
1988,117.5
1988,118
1988,118.5
1988,119
1988,119.8
1988,120.2
1988,120.3
1988,120.5
1989,121.1
1989,121.6
1989,122.3
1989,123.1
1989,123.8
1989,124.1
1989,124.4
1989,124.6
1989,125
1989,125.6
1989,125.9
1989,126.1
1990,127.4
1990,128
1990,128.7
1990,128.9
1990,129.2
1990,129.9
1990,130.4
1990,131.6
1990,132.7
1990,133.5
1990,133.8
1990,133.8
1991,134.6
1991,134.8
1991,135
1991,135.2
1991,135.6
1991,136
1991,136.2
1991,136.6
1991,137.2
1991,137.4
1991,137.8
1991,137.9
1992,138.1
1992,138.6
1992,139.3
1992,139.5
1992,139.7
1992,140.2
1992,140.5
1992,140.9
1992,141.3
1992,141.8
1992,142
1992,141.9
1993,142.6
1993,143.1
1993,143.6
1993,144
1993,144.2
1993,144.4
1993,144.4
1993,144.8
1993,145.1
1993,145.7
1993,145.8
1993,145.8
1994,146.2
1994,146.7
1994,147.2
1994,147.4
1994,147.5
1994,148
1994,148.4
1994,149
1994,149.4
1994,149.5
1994,149.7
1994,149.7
1995,150.3
1995,150.9
1995,151.4
1995,151.9
1995,152.2
1995,152.5
1995,152.5
1995,152.9
1995,153.2
1995,153.7
1995,153.6
1995,153.5
1996,154.4
1996,154.9
1996,155.7
1996,156.3
1996,156.6
1996,156.7
1996,157
1996,157.3
1996,157.8
1996,158.3
1996,158.6
1996,158.6
1997,159.1
1997,159.6
1997,160
1997,160.2
1997,160.1
1997,160.3
1997,160.5
1997,160.8
1997,161.2
1997,161.6
1997,161.5
1997,161.3
1998,161.6
1998,161.9
1998,162.2
1998,162.5
1998,162.8
1998,163
1998,163.2
1998,163.4
1998,163.6
1998,164
1998,164
1998,163.9
1999,164.3
1999,164.5
1999,165
1999,166.2
1999,166.2
1999,166.2
1999,166.7
1999,167.1
1999,167.9
1999,168.2
1999,168.3
1999,168.3
2000,168.8
2000,169.8
2000,171.2
2000,171.3
2000,171.5
2000,172.4
2000,172.8
2000,172.8
2000,173.7
2000,174
2000,174.1
2000,174
2001,175.1
2001,175.8
2001,176.2
2001,176.9
2001,177.7
2001,178
2001,177.5
2001,177.5
2001,178.3
2001,177.7
2001,177.4
2001,176.7
2002,177.1
2002,177.8
2002,178.8
2002,179.8
2002,179.8
2002,179.9
2002,180.1
2002,180.7
2002,181
2002,181.3
2002,181.3
2002,180.9
2003,181.7
2003,183.1
2003,184.2
2003,183.8
2003,183.5
2003,183.7
2003,183.9
2003,184.6
2003,185.2
2003,185
2003,184.5
2003,184.3
2004,185.2
2004,186.2
2004,187.4
2004,188
2004,189.1
2004,189.7
2004,189.4
2004,189.5
2004,189.9
2004,190.9
2004,191
2004,190.3
2005,190.7
2005,191.8
2005,193.3
2005,194.6
2005,194.4
2005,194.5
2005,195.4
2005,196.4
2005,198.8
2005,199.2
2005,197.6
2005,196.8
2006,198.3
2006,198.7
2006,199.8
2006,201.5
2006,202.5
2006,202.9
2006,203.5
2006,203.9
2006,202.9
2006,201.8
2006,201.5
2006,201.8
2007,202.416
2007,203.499
2007,205.352
2007,206.686
2007,207.949
2007,208.352
2007,208.299
2007,207.917
2007,208.49
2007,208.936
2007,210.177
2007,210.036
2008,211.08
2008,211.693
2008,213.528
2008,214.823
2008,216.632
2008,218.815
2008,219.964
2008,219.086
2008,218.783
2008,216.573
2008,212.425
2008,210.228
2009,211.143
2009,212.193
2009,212.709
2009,213.24
2009,213.856
2009,215.693
2009,215.351
2009,215.834
2009,215.969
2009,216.177
2009,216.33
2009,215.949
2010,216.687
2010,216.741
2010,217.631
2010,218.009
2010,218.178
2010,217.965
2010,218.011
2010,218.312
2010,218.439
2010,218.711
2010,218.803
2010,219.179
2011,220.223
2011,221.309
2011,223.467
2011,224.906
2011,225.964
2011,225.722
2011,225.922
2011,226.545
2011,226.889
2011,226.421
2011,226.23
2011,225.672
2012,226.665
2012,227.663
2012,229.392
2012,230.085
2012,229.815
2012,229.478
2012,229.104
2012,230.379
2012,231.407
2012,231.317
2012,230.221
2012,229.601
2013,230.28
2013,232.166
2013,232.773
2013,232.531
2013,232.945
2013,233.504
2013,233.596
2013,233.877
2013,234.149
2013,233.546
2013,233.069
2013,233.049
2014,233.916
2014,234.781
2014,236.293
2014,237.072
2014,237.9
2014,238.343
2014,238.25
2014,237.852
2014,238.031
2014,237.433
2014,236.151
2014,234.812
2015,233.707
2015,234.722
2015,236.119
2015,236.599
2015,237.805
2015,238.638
2015,238.654
2015,238.316
2015,237.945
2015,237.838
2015,237.336
2015,236.525
2016,236.916
2016,237.111
2016,238.132
2016,239.261
2016,240.229
2016,241.018
2016,240.628
2016,240.849
2016,241.428
2016,241.729
2016,241.353
2016,241.432
2017,242.839
2017,243.603
2017,243.801
2017,244.524
2017,244.733
2017,244.955
2017,244.786
2017,245.519
2017,246.819
2017,246.663
2017,246.669
2017,246.524
2018,247.867
2018,248.991
2018,249.554
2018,250.546
2018,251.588
2018,251.989
2018,252.006
2018,252.146
2018,252.439
2018,252.885
2018,252.038
2018,251.233
2019,251.712
2019,252.776
2019,254.202
2019,255.548
2019,256.092
2019,256.143
2019,256.571
2019,256.558
2019,256.759
2019,257.346
2019,257.208
2019,256.974
2020,257.971
2020,258.678
2020,258.115
2020,256.389
2020,256.394
2020,257.797
2020,259.101
2020,259.918
2020,260.28
2020,260.388
2020,260.229
2020,260.474
2021,261.582
2021,263.014
2021,264.877
2021,267.054
2021,269.195
2021,271.696
2021,273.003

4

Ah, I think the magnitude of your features are simply too large for you to be able to “see” any changes in the cost function. The features you are plugging into qml.Displacement — the first argument in qml.Displacement — are the X values, which are years on the order of 1000. Try measuring everything w.r.t. the smallest year (1913), i.e., subtract 1913 from the X data.

5

Thank you, that worked. I am focusing on the training accuracy and the parameters to optimize. Thanks for your help!

6

Awesome! Glad that worked :rocket:

7

I wanted your guidance. The Prediction curve plotted seems pretty flat compared to the CPI values which show an upward trend year after year (as shown in the image below)
The cost function varied till about 250 iterations and then remained stuck at one value. Do you have recommendations on which parameters in the code should I change to get closer to the actual trend.
image
Thank you as always for your prompt response.

8

Hey @NolanCMas, this is the age-old question in machine learning! The performance of your model depends on several things including, but not limited to:

  • the number of parameters in your model
  • the functional form of the model itself (e.g. a CNN or a GAN, for example)
  • your optimizer
  • your optimizer’s hyperparameters (momentum, decay, etc.)
  • other hyperparameters like learning rate, batch size, etc.
  • how much data you have

It’s quite a tedious process to figure out what the right combination of all of these things is, but that’s the way it goes!

As a first step, though, I would first try different optimizers :slight_smile:.

9

It could also be that your model isn’t quite right for this application. Maybe you want something that is used for natural language processing and/or time-series data? In models built for those applications, there’s some degree of chronological correlation between datapoints built into them. That might help over a standard QNN!